SHAttered Collision Attack: uno sguardo alla collisione SHA1 ed al mondo degli hash
“In informatica una funzione crittografica di hash è un algoritmo matematico che trasforma dei dati di lunghezza arbitraria (messaggio) in una stringa binaria di dimensione fissa chiamata valore di hash, impronta del messaggio o somma di controllo, ma spesso anche con il termine inglese message digest.” – https://it.wikipedia.org/wiki/Funzione_crittografica_di_hash
Esempio di funzione di hash con SHA1
Quindi significa che se applico una funzione di hash a qualcosa l’output sarà un codice esadecimale di lunghezza fissa, esempio:
hash("ciao") = 1E4E888AC66F8DD41E00C5A7AC36A32A9950D271
hash("ciau") = 927B2387A3E4C2CD101DEFC7537D3ECAEBB8151D
In quest’esempio è stato usato l’algoritmo di hash denominato SHA1.
Il problema è che se mappiamo l’universo infinito su un universo finito, sicuramente due elementi diversi avranno lo stesso codice hash, perché per quanto grande lo spazio, l’insieme di codici disponibili, non potranno mai essere infiniti, per esempio SHA1 ha un numero di 2^160 codici diversi, che è un numero pari a: 1,4615016373309029182036848327163e+48 ma sicuramente minore dell’infinito.
N.B.: L(lunghezza)= X bits , 4 bits (nibble) sono una cifra Hex quindi X/4=numero cifre esadecimali generate.
SHA1: L=160 bits genera una stringa di 160/4=40 caratteri esadecimali.
Principio dei buchi della colombaia e collisione degli hash
Se abbiamo C colombi e B buchi nella colombaia, con C=B allora ogni colombo avrà il suo buco dove mettersi, ma se C>B allora almeno due colombi dovranno condividere la stessa buca, esempio: 11 colombi e 10 buchi, due colombi vivranno insieme.
Nel mondo degli hash possiamo tradurlo così, se abbiamo 2^161 messaggi e l’algoritmo è a 160 bit, avremo che 2^161/2^160 = 2^(161-160) = 2^1 =2 ad ogni hash code saranno associati 2 messaggi diversi, quindi non vi è più la corrispondenza univoca di un codice hash diverso per ogni messaggio.
Attacco del compleanno: Probabilità di collisione negli hash
Questa riflessione ci porta a pensare che comunque è veramente improbabile, che due elementi diversi tra loro possano generare due codici uguali, si parla di calcolo della probabilità basata sull’attacco del compleanno, ossia il calcolo probabilistico di quante persone possono esser nate nello stesso giorno.
Senza addentraci in complessi passaggi matematici approssimiamo questa probabilità al valore: 2^(n/2) che nel caso di SHA1 è 2^(80), che comunque è un numero grande, cioè significa che per avere una collisione al 50% ci basta generare 1208925819614629174706176 (circa 1,2*10^24) messaggi diversi.
Il punto è riuscire a creare due messaggi diversi, intellegibili che hanno hash uguali.
Il calcolo dell’hash avviene suddividendo il messaggio in blocchi di misura fissa con eventuale zero padding sull’ultimo se non raggiunge la lunghezza del blocco, ossia lo si riempie aggiungendo degli zeri, quindi si applicano delle funzioni matematiche, fino a giungere al calcolo del codice hash di lunghezza fissa a seconda dei bit dell’algoritmo.
Creare due messaggi diversi con lo stesso hash
L’idea sarebbe quella di creare due messaggi che diano lo stesso hash, così che quando qualcuno applica la funzione di hash per “firmarlo” o “garantirlo”, si potrebbe sostituire quel messaggi con l’altro, rimanendo sicuri che genererà lo stesso codice hash, chiaramente se si utilizza un algoritmo differente, da quello previsto per la collisione, i due hash saranno differenti.
Ma questo è un processo complesso, lungo, difficile ed applicabile a singole entità o file, infatti ciò che vale per un file, non vale più se quello stesso file viene inserito in un ambiente come ad esempio una pendrive o un hard disk, dato che il calcolo dei blocchi inizierebbe da un punto diverso.
FILE1 (composto dai blocchi B1, B2, B3, B4) —> modifico i blocchi B2 e B4 –> ottengo FILE2 (B1, M2, B3, M4)
HASH(FILE1)=HASH(FILE2)
Ma se FILE1 è in un disco HD(D1,D2,D3,…D9999) il cui HASH(HD)=ABC123
se sostituissi FILE1 con FILE2 nel disco HD, otterrei HASH(HD)=BFD75A
insomma l’hash del disco cambierebbe, perché la collisione è studiata solo per FILE1 e FILE2 partendo dai loro blocchi interni, mentre il calcolo dell’hash di tutto il disco HD, partirebbe dal blocco D1, sballando così tutta l’artefazione relativa ai due file.
(video con esperimento: https://www.youtube.com/watch?v=53B_0WJHPRA)
Tipi di attacchi sui codici hash
Gli attacchi sui codici hash sono:
- COLLISIONE: dati due messaggi diversi di cui non conosciamo l’hash, dobbiamo fare in modo da ottenere due hash uguali: m1 ed m2 -> h(m1)=h(m2). (resistenza forte alle collisioni)
- PRE-IMAGE DI PRIMO TIPO: dato un codice hash noto, dobbiamo trovare un messaggio m, tale che hash(m)=h-noto.(non invertibilità delle funzioni di hash)
- PRE-IMAGE DI SECONDO TIPO: dato un messaggio noto m1 e calcolato il suo hash H(m1), dobbiamo trovare un m2 diverso da m1 che restituisce lo stesso hash di m1. (resistenza debole alle collisioni)
Il PRE-IMAGE DI SECONDO TIPO sarebbe veramente rischioso, se fosse possibile effettuarlo in pratica, cosa che ancora non è effettuabile e sicuramente non su oggetti come gli hard disk o big data.
Infatti se facessimo una copia forense bit a bit di un disco e calcolassimo l’hash, potremmo modificare qualcosa nel disco tale per cui l’hash ricalcolato sarebbe identico a quello pre-modifica.
SHAttered Attack: La collisione SHA1
Dopo questa lunga premessa passiamo ad analizzare il caso SHATTERED (https://security.googleblog.com/2017/02/announcing-first-sha1-collision.html) dei due file PDF diversi tra loro, leggibili ma con hash SHA1 identici.
I due file si possono prelevare da qui:

Come si vede dall’immagine sono due PDF identici, salvo per il colore di sfondo, il file shattered-1.pdf è celeste mentre shattered-2.pdf è rosso, però i due codici SHA1 sono identici:
shattered-1.pdf - SHA1: 38762CF7F55934B34D179AE6A4C80CADCCBB7F0A shattered-2.pdf - SHA1: 38762CF7F55934B34D179AE6A4C80CADCCBB7F0A
ma se già facciamo l’MD5 dei due:
shattered-1.pdf - MD5: EE4AA52B139D925F8D8884402B0A750C shattered-2.pdf - MD5: 5BD9D8CABC46041579A311230539B8D1
Ecco perchè il sistema migliore per garantire la non collisione, non è tanto applicare un algoritmo che ancora non è stato computazionalmente sottomesso alla collisione, visto che sappiamo che tutti gli algoritmi lo sono potenzialmente soggetti, ma applicare due algoritmi differenti, ciò che è stato forgiato per “imbrogliare” uno non vale per l’altro.
Sotto il cofano di SHAttered: Analisi tecnica
Utilizzando l’editor esadecimale wxHexEditor V. 0.22 presente nella distribuzione GNU/Linux CAINE 8.0, possiamo caricare entrambi i file e verificare dove sono diversi:
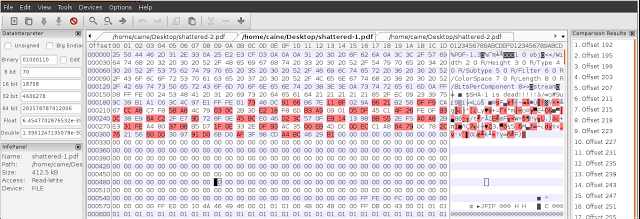
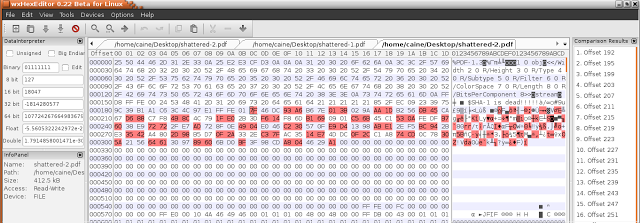
Offset decimale dei bytes differenti: dal 192 al 319.
Se proviamo ad incollare i bytes differenti di Shattered-2.pdf sui byte corrispondenti di Shatterd-1.pdf, si otterrà che Shattered-1.pdf sarà identico anche nel colore a Shattered-2.pdf e l’hash continuerà ad essere quello.
Insomma una manciata di bytes, messi nel posto giusto hanno creato la collisione SHA1, sembra facile, visto così, in fondo sono pochi byte, ma sappiamo che è stata utilizzata una potenza di calcolo straordinaria, pertanto non me la sento di dire addio per tutto a SHA1, almeno per ora…
A cura di: Nanni Bassetti

Dott. Giovanni Bassetti, laureato in Scienze dell’Informazione, iscritto all’Albo dei Consulenti Tecnici presso il Tribunale Civile di Bari al n. 17, Project Manager della Live Distro internazionale CAINE per le indagini informatiche forensi, nonché fondatore della comunità italiana online dedicata alle investigazioni digitali (Computer Forensics Italy), autore di numerosi articoli pubblicati su riviste del settore nazionali ed internazionali. È stato consulente per alcuni procedimenti penali di rilevanza nazionale, è autore di un testo sulla computer forensics ed è segretario e membro fondatore di ONIF (Osservatorio Nazionale Informatica Forense).
Inoltre, ha partecipato come relatore e docente a numerosi convegni e corsi nazionali ed internazionali dedicati all’informatica forense ed intelligenza artificiale.