Secret sharing: come mantenere un segreto pur condividendolo con più soggetti

Nella vita reale, quando due persone conoscono un segreto, sappiamo che non può più essere considerato un segreto. Nel mondo digitale, grazie al ‘secret sharing”, le cose possono andare diversamente. Vediamo come e testiamo un esempio del sistema che ci permette di condividere segreti in modo sicuro tra più soggetti.

“Quando due persone conoscono un segreto, non è più un segreto”, cita una famosa frase di Roberto Calvi, ultimo presidente del Banco Ambrosiano di Milano, ripresa poi nel film “Le conseguenze dell’amore” di Paolo Sorrentino. Concetto piuttosto semplice ma di una solidità incontrastabile: condividendo un segreto con una o più persone se ne perde il controllo, il segreto può essere divulgato senza il nostro consenso e senza che potenzialmente ne veniamo in alcun modo a conoscenza.

Questo ovviamente vale nella vita reale, dove la matematica trova spesso difficile applicazione nei rapporti tra le persone che invece vengono regolati da principi e regole comportamentali diverse basate sulla fiducia. Nel mondo digitale, fortunatamente, possiamo trovare soluzioni che superano i rapporti fiduciari costruendo le regole su principi matematici e algoritmi.

Per poter condividere un segreto tra più soggetti, infatti, sono state ideate diverse soluzioni, tutte finalizzate a impedire a un singolo elemento del gruppo di poter divulgare le informazioni riservate senza il consenso (o la collaborazione) di altri membri del gruppo. In sostanza, si vuole far sì che un segreto rimanga un segreto anche se conosciuto da più persone, a meno che queste (o una parte di queste stabilita a priori) non si sia accordata per “sbloccare” il segreto e rendere pubbliche le informazioni.

Una delle modalità più interessanti d’implementazione di un algoritmo di condivisione di segreti tra soggetti diversi è quella proposta da Adi Shamir, crittografo israeliano già noto per essere stato co-autore dell’algoritmo a chiave pubblica RSA insieme a Ron Rivest e Len Adleman. La lettera “S” in “RSA” è infatti proprio l’iniziale del suo nome, che quindi probabilmente molti di noi conoscono senza averlo mai associato agli algoritmi di condivisione segreti ma soltanto al noto sistema di cifratura asimmetrica.

Shamir si è posto il problema di come poter condividere un segreto tra un numero ‘n’ di persone in modo tale che per poterlo “svelare” debbano essere presenti e concordi almeno un numero ‘k’ di persone, inferiore o uguale a ‘n’.

Semplifichiamo con un esempio: i pirati e lo scrigno sepolto

In sostanza, immaginiamo che tre pirati vogliano mantenere segreto il punto esatto di un tratto di spiaggia sotto il quale è sepolto uno scrigno, con la condizione che nessuno sia in grado di andare da solo a scavare ma nello stesso tempo che la scomparsa di uno dei tre non impedisca ai due rimanenti di appropriarsi del bottino. Non possono dividere la mappa con le coordinate in tre, perché da un lato, non è garantito che due di loro saranno in grado d’interpretarla, dall’altro uno da solo potrebbe avere elementi sufficienti per scoprire il punto in cui scavare.

Molto semplicemente, possono tracciare con uno spago una retta che interseca la spiaggia nel punto in cui è sotterrato il tesoro e posizionarsi ognuno su un punto della retta, distanti in modo da non vedere dove sono posizionati gli altri, segnandosi ognuno le coordinate del suo punto. Abbiamo quindi tre punti (le coordinate dei tre pirati) lungo i quali passa una retta (lo spago teso) che interseca la spiaggia in un punto esatto (il tesoro).

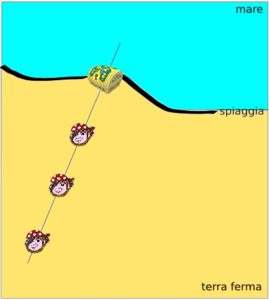
Si comincia a questo punto a scoprire il “trucco”: se due pirati vogliono recuperare il tesoro senza coinvolgere il terzo, possono autonomamente posizionarsi nei due punti loro assegnati, tendere uno spago e farlo proseguire diritto verso la spiaggia, intersecando così il punto in cui scavare. Non serve il terzo pirata, che aggiungerebbe un punto “inutile” sulla stessa retta. Non importa quale pirata manca e quali due sono presenti, sono tutti intercambiabili per raggiungere lo scopo d’intersecare con lo spago la spiaggia. Un pirata da solo, nello stesso tempo, non avrebbe idea di dove “fissare” la retta che passa verso di lui, avendo tutti i 360 gradi di rotazione a disposizione, mantenendo così il segreto… un segreto fino a che non riesce a trovare un altro pirata.

Utilizzi pratici del sistema

L’algoritmo di Shamir (e algoritmi che risolvono problemi simili) hanno numerose applicazioni pratiche. Ad esempio, vengono utilizzati pesantemente nel mondo delle criptomonete per generare portafogli definiti “multisig”, nei quali per poter spendere il contenuto di un indirizzo è necessario che siano presenti più partecipanti contemporaneamente. Il wallet è in questo modo “blindato” perché nessun singolo sarà mai in grado di svuotarlo. In alcuni casi, uno dei partecipanti può essere l’exchange stesso (così come avviene, ad esempio, con il wallet GreenAddress) rendendo quindi la sua presenza indispensabile per poter disporre dei fondi (con possibilità di sblocco in caso di scomparsa dell’exchange) ma, nello stesso tempo, garantendo gli utilizzatori circa il fatto che l’exchange da solo non è in grado di sottrarre criptomoneta.

In ambito di sequestro di criptomoneta, anche, la proprietà di condivisione sicura di chiavi dei wallet è un elemento strategico, per non lasciare la responsabilità delle, spesso enormi, cifre sequestrate al singolo operatore. Una volta creato il wallet di destinazione dei fondi sequestrati, chiunque può proseguire con le attività di raccolta dei fondi e trasferimento verso di esso, ma il dissequestro (o l’accesso ai fondi, per qualunque motivò) sarà consentito soltanto ai membri del gruppo nominato dall’Autorità. Questo tutela non soltanto il proprietario dei fondi sequestrati, ma anche gli operatori, che quindi non potranno mai essere coinvolti in eventuali fuoriuscite di fondi, né tentati a farlo personalmente, come purtroppo si è visto in alcune indagini oltreoceano relative ai Black Market a seguito delle quali si è scoperto come parte delle criptomonete dell’indagato erano finite nei wallet di qualche operatore, convinto di poterla fare franca.

In ambito di sicurezza informatica, spesso è necessario custodire segreti con condizioni tali per cui l’apertura degli stessi deve avvenire solamente in presenza di un certo numero di soggetti. Possiamo parlare di file di log di sistemi con dati sensibili, dati di traffico, persino password, credenziali, “seed” di sistemi crittografici. Tutti dati che possono essere intesi come accedibili soltanto a più di una persona.

Immaginiamo poi, in ambito giudiziario, la situazione in cui un certo numero di periti vogliono poter accedere a dei dati solo quando sono tutti presenti e, nel contempo, si vuole tollerare l’assenza di uno o due periti che potrebbero non essere disponibili. Non è sufficiente suddividere la password con la quale sono stati cifrati i dati in “n” pezzi, anche creando sovrapposizioni, perché se non fatto con le dovute attenzioni rischierebbe di fornire a un gruppo inferiore al minimo stabilito la possibilità di accedere ai dati o, dall’altra parte, di richiedere più persone di quelle effettivamente disponibili durante un incontro.

Sono persino allo studio da anni sistemi d’intercettazione che archivino quanto acquisito dalle sonde (es. telefonate, traffico telematico, etc…) in modo che gli operatori non siano in grado – da soli – di accedere al materiale intercettato, rendendo invece indispensabile la presenza, ad esempio, di un Magistrato o un Giudice. Una delle questioni cardine delle attività d’intercettazione – spesso citate dai legali e dai fautori della privacy – è proprio il fatto che è corretto che la Giustizia operi attività d’ispezione anche all’insaputa dei soggetti coinvolti, è meno corretto che qualcuno possa autonomamente visionare tale materiale. Una soluzione come il Secret Sharing di Shamir risolverebbe in modo matematico questo problema, garantendo la tutela della privacy e la riservatezza dei dati acquisiti, utilizzabili sì ma sotto determinate condizioni.

Proviamo in pratica l’algoritmo di Shamir

L’algoritmo di Adi Shamir implementa – in modo scalabile su gruppi e membri variabili – proprio il sistema di condivisione di segreti accennato sopra. Il vincolo del codice è proprio quello di rendere determinabile in modo certo un segreto se sono presenti almeno k elementi su un gruppo di n, ma indeterminabile se non viene raggiunto il numero minimo di partecipanti.

Per chiarire dal punto di vista tecnico il funzionamento dell’algoritmo, ne abbiamo sviluppato una semplice applicazione (per semplice uso didattico, quindi non priva d’imperfezioni) pubblicandola per chi vuole cimentarvisi al link https://github.com/nannib/crypto/blob/master/shamir_nb.py.

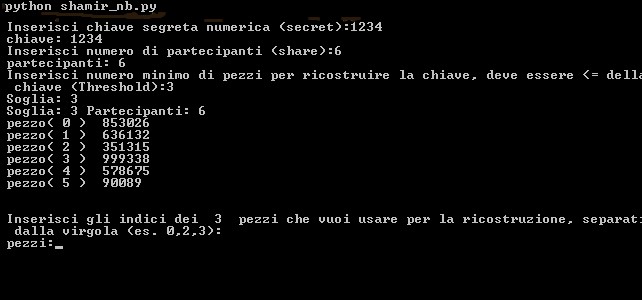
Il codice si apre con l’inserimento della chiave segreta S₀, si inserisce il numero di “shares” (ossia quanti membri del gruppo avranno un pezzo della chiave ed infine il numero minimo di partecipanti (soglia) che servono per ricostruire la chiave.

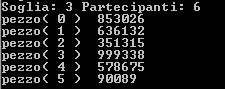
Ad esempio, scegliamo come chiave segreta “1234”, come membri del gruppo decidiamo di avere sei persone e come numero minimo necessario per “sbloccare” il segreto ne impostiamo almeno tre. Quindi se anche tre persone dovessero mancare, con quest’impostazione ne saranno sufficienti tre per ricostruire la chiave.

Esempio:

Chiave:1234
Partecipanti:6
Numero minimo: 3

Nel programma è impostato un numero primo abbastanza grande:

Si passa quindi alla scelta casuale dei coefficenti del polinomio, presi tra 0 e p-1

Dato che sembra tutto troppo facile, osserviamo un attimo la formula matematica:

f(x)=S₀+r₀x¹+r₁x²+…+r_k-1x^(k-1)

 Nella funzione f(x), S₀ è la chiave segreta, gli r sono i coefficienti e alle x possiamo assegnare numeri arbitrari (1, 2, 3, etc…). Se calcoliamo f(0), cioè alla x assegniamo il valore ‘0’, otteniamo f(0)=S₀ perché tutti gli altri componenti del polinomio si azzerano.

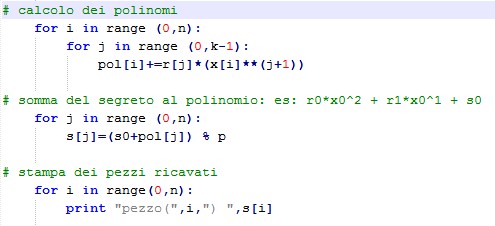
Al fine di dividere la chiave segreta dobbiamo calcolare i polinomi per ogni valore di X relativo a ciascun partecipante, quindi se abbiamo 6 partecipanti dobbiamo calcolare f(1), f(2), f(3), f(4), f(5), f(6) per x=1, 2, 3, 4, 5 e 6.

Il programma genera i polinomi da sommare a S₀ e calcolare il modulo col numero primo p:

A questo punto abbiamo i pezzi (le cosiddette “shares”) per tutti i partecipanti,

Adesso, cerchiamo di ricostruire il codice segreto: per ricavare la chiave servono almeno k partecipanti, che nel nostro esempio abbiamo impostato a tre. Con meno di tre soggetti, non sarà possibile in alcun modo ricavare la chiave, questo perché quando abbiamo generato i singoli pezzi, abbiamo impostato che la soglia minima doveva essere quel numero. Se avessimo voluto permettere a un numero inferiore di partecipanti di ottenere il segreto, sarebbe bastato impostare a ‘2’ il parametro.

La ricostruzione avviene tramite interpolazione di Lagrange, che nell’implementazione pratica per X=0 diventa così:

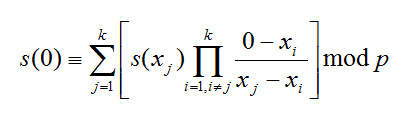
Quindi passiamo a calcolare prima la produttoria:

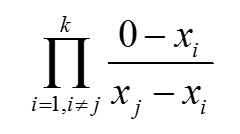
In seguito calcoliamo il prodotto intero del pezzo per la produttoria relativa, quindi pezzo(1) * produttoria(1), pezzo(2)*produttoria(2), ecc.

Infine, calcoliamo la sommatoria dei vari SS[i] ed il modulo con P:

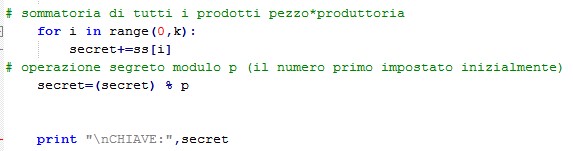
Si ottiene, a questo punto, il segreto originale “1234” a patto che appunto il numero di partecipanti sia almeno quanto è stato impostato durante la creazione come minimo necessario per lo “sblocco”.

 

Articolo a cura di Paolo Dal Checco e Nanni Bassetti