CURVEBALL, la vulnerabilità in Microsoft CryptoAPI
Di recente si è creata molta agitazione intorno alla notizia riguardante la scoperta di una falla critica all’interno di Windows 10.
Falla ad oggi già chiusa tramite il primo Patch Tuesday del 2020, rilasciato il 14 gennaio, tramite le correttive presenti a questo link.
La notizia ha avuto un’eco globale, dopo che il noto ricercatore Brian Krebs, il 13 gennaio, ha postato sul proprio blog un tweet di Will Dormann[1] contenente la seguente affermazione:
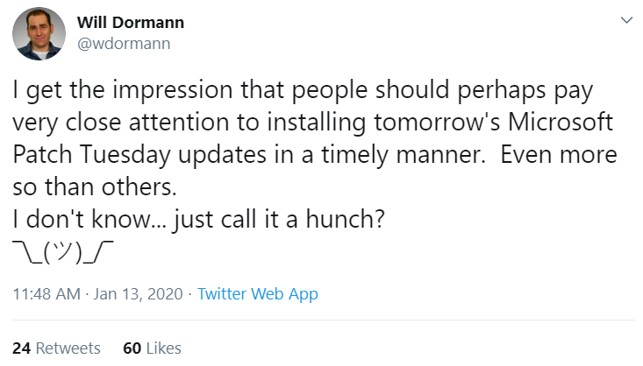
A poche ore di distanza, la KrebsOnSecurity[2] ha ricevuto un avviso direttamente dalla National Security Agency (NSA) americana contenente una dichiarazione attestante che il direttore della sicurezza informatica dell’NSA Anne Neuberger avrebbe avuto in programma un contatto con i media il giorno successivo (14 gennaio) nel quale avrebbe “fornito una notifica dettagliata riguardante un attuale problema di sicurezza informatica globale, scoperto dall’NSA”.
Il resto è storia.
Quello che c’è realmente dietro al coinvolgimento dell’NSA sconfina quasi nel gossip: pare che sia Microsoft sia la stessa NSA fossero da tempo a conoscenza della vulnerabilità. Per di più, sembra che avessero già provveduto a fornire le correttive software con largo anticipo e in totale segretezza solo a un gruppo ristretto di partner tecnologici statunitensi. Il perché, almeno per le vie ufficiali, non è dato saperlo.
Ma cos’ha questa vulnerabilità di tanto importante da aver avuto risvolti da soap opera e questa eco smisurata?
LA VULNERABILITÀ
In sostanza, il bug insiste su una componente di Windows nota come crypt32.dll, un modulo che gestisce le funzioni di messaggistica crittografica e di certificazione nell’architettura Microsoft CryptoAPI[3].
CryptoAPI, quindi, fornisce servizi che consentono agli sviluppatori di proteggere le applicazioni Windows che utilizzano la crittografia, e include funzionalità per crittografare e decrittografare i dati utilizzando certificati digitali.
Una vulnerabilità critica in questo componente di Windows potrebbe avere implicazioni di sicurezza ad ampio raggio per una serie di importanti funzioni di Windows, tra cui:
- autenticazione su Windows 10;
- autenticazione su Windows Server 2016/2019;
- protezione dei dati sensibili gestiti dai browser Microsoft Internet Explorer / Edge;
- applicazioni e strumenti di terze parti.
Non meno importante, questo difetto in crypt32.dll potrebbe anche essere utilizzato per emulare una qualsivoglia firma digitale per firmare un software specifico. Tale debolezza permetterebbe a un aggressore di mascherare un malware in un programma benigno, come se fosse prodotto e firmato da una società di software legittima.
CURVEBALL
Il bug – che alcuni hanno iniziato a chiamare #CurveBall – ha un impatto sulla libreria crypt32.dll di Windows, la quale non implementa correttamente il meccanismo di crittografia delle curve ellittiche (ECC).
Seguendo la terminologia del blog Nick Sullivan di Cloudflare, la crittografia ECC può essere descritta come un’implementazione bizzarra del gioco del biliardo.
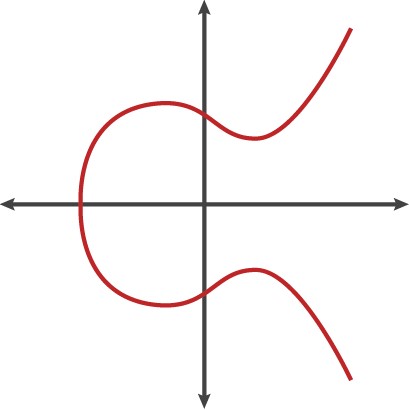
y² = x³ + ax + b
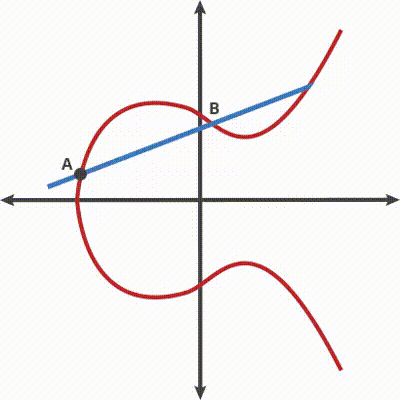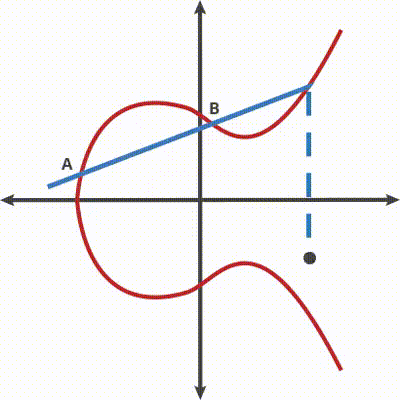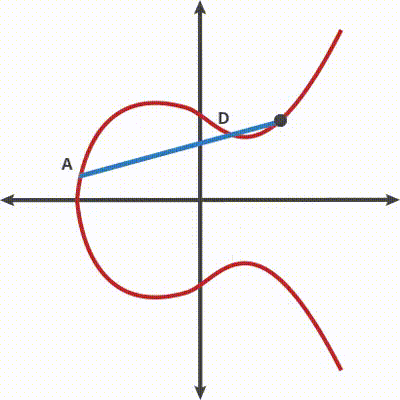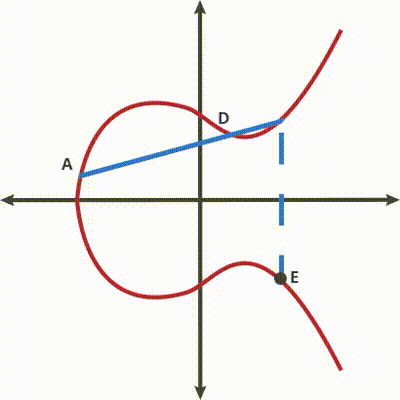
Consideriamo la curva ellittica, descritta con l’equazione y² = x³ + ax + b, come il nostro tavolo da biliardo.
Aggiungendo due punti sulla curva, A e B, possiamo considerarli come il tragitto della pallina da biliardo a seguito della nostra scoccata. Quindi, per ottenere la traiettoria A B, possiamo posizionare la palla nel punto A e tirala verso il punto B.
Algoritmo ECC su tavolo da biliardo
Come regola, quando la palla colpisce la curva, essa rimbalza o verso l’alto (se è sotto l’asse x), o dritta verso il basso (se è sopra l’asse x) verso l’altro lato della curva. In questo secondo caso il risultato è dato da C.
Si può iterare il meccanismo secondo questo algoritmo per un numero n di volte[4] a proprio piacere.
Quindi, facendo finta di essere un giocatore: eseguiamo dei colpi partendo da un punto P iniziale, per n volte.
Un avversario, che entra nella nostra stanza al termine dei nostri colpi, può visionare la posizione finale della palla, ma non ha alcun modo di dedurre quante volte è stata colpita prima di arrivare lì, né da dove sia partita. Potrebbe tentare di provare tutti i punti di partenza possibili, fino a indovinare P e le n iterazioni, ma tale approccio è proprio la forza dell’algoritmo: facile da eseguire ma computazionalmente difficile da invertire.
In termini più matematici, calcolare n * P su curve ellittiche è estremamente facile. Tuttavia, dati n * P e P è difficile determinare n.
DIFFIE-HELLMAN A CURVA ELLITTICA: DOPPIO BILIARDO
L’algoritmo Elliptic-Curve Diffie-Hellman (ECDH) estende ulteriormente questo concetto e utilizza l’impossibilità di “indovinare” il numero di volte che la palla è stata colpita al fine di creare un segreto condiviso tra due parti (Alice e Bob) in presenza di un attaccante (Eve).
In questo algoritmo il gioco è doppio.
Alice gioca sul biliardo da sola in una stanza: inizia posizionando la palla in un punto noto P e colpendo S₁ volte (S₁ * P) a sua scelta. Quando Alice ha finito, manda una foto del tavolo a Bob. Bob posiziona la palla nello stesso punto sul suo tavolo (S₁ * P) secondo l’immagine e poi colpisce S₂ volte (S₂ * (S₁ * P)).
Allo stesso tempo, Bob inizia una nuova partita su un altro tavolo e colpisce S₂ volte (S₂ * P), inviando una foto ad Alice in modo che possa colpire S₁ volte. (S₁ * (S₂ * P)).
A questo punto entrambi possono usare la coordinata X di questo punto finale come segreto condiviso.
In una notazione più formale: S₁, S₂ sono chiamate chiavi segrete, mentre S₁ * P, S₂ * P sono chiamate chiavi pubbliche e indicate come Pb₁ e Pb₂.
In questo processo né Alice né Bob hanno appreso i reciproci segreti. Ancora più importante, Eve non ha modo di desumere i colpi S₁ ed S₂, la posizione finale del tavolo e del conseguente segreto condiviso, sebbene abbia avuto accesso alle immagini intermedie del tavolo, scambiate nel mezzo del gioco.
IL BUG
Ma Eve non è del tutto spacciata: sebbene non riesca a ottenere il segreto condiviso semplicemente intercettando gli interscambi, può attivamente confondere le immagini inviate tra Alice e Bob in modo da poter creare calcoli sbagliati, volti a ottenere le coordinate del segreto condiviso.
Tale rischio di intercettazione era già ben noto ai tempi della progettazione dei meccanismi di pairing nel protocollo Bluetooth: ai tempi è stato risolto tramite l’aggiunta di un ulteriore livello di protezione, in modo da poter verificare che le coordinate X dei punti relativi alle chiavi pubbliche condivise (le “immagini” del tavolo da biliardo) non siano stati contraffatti tramite MITM. Tale protocollo è lo stesso ripreso da Microsoft in crypt32.dll.
Tuttavia, entrambi i protocolli non impongono alcuna verifica sulle coordinate Y del piano! E questo è il punto di debolezza utilizzato per rompere il meccanismo di sicurezza ECC.
Eve può sfruttare questa debolezza è cambiando le “immagini” del tavolo, posizionando la palla (chiave pubblica) in un punto molto speciale del tavolo.
In termini matematici, Eve sta azzerando la coordinata Y delle chiavi pubbliche scambiate da Alice e Bob. Dal momento che le coordinate Y non sono verificate, il gioco di Eve è siffatto.
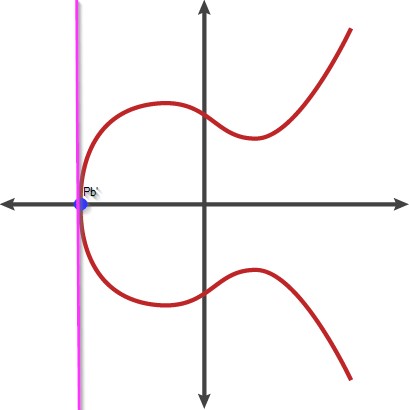
La chiave pubblica manipolata (Pb’) è posizionata sull’asse X. La sua tangente è una linea retta
Tornando al tavolo da biliardo: di solito, se tentiamo più volte di tirare la palla verso uno stesso punto, la palla può colpire la curva con vari tipi di angoli, cambiando posizione a ogni tiro senza mai passare più di una volta sui punti già attraversati.
Ma, quando posizioniamo la palla sull’asse X (Pb’) e la scocchiamo ripetutamente, andrà sempre nella stessa direzione, rendendo il gioco estremamente noioso. Di fatto la retta generata (tangente) non si intersecherà mai con la curva, quindi la “palla” sarà fermata “artificialmente” su un punto chiamato “punto all’infinito” o ∞. Nel tiro successivo, la palla verrà lanciata verso il punto di originaria Pb’, terminando lì la sua corsa.
I tiri successivi semplicemente ripetono questo processo. Ad ogni iterazione la palla o raggiunge ∞, o ritorna sull’asse X a Pb’.
Quindi a Eve basta sostituire le immagini originali (Pb₁, Pb₂) dei rispettivi tavoli con le immagini “fisse” (Pb₁’, Pb₂’): se entrambi S₁, S₂ sono pari, allora il risultato sarà S₂ * Pb₁ ‘= ∞ = S₁ * Pb₂’.
Di conseguenza, l’associazione avrà esito positivo e creerà una chiave condivisa che Eva conosce. In ogni altro caso, vale a dire se S₁ o S₂ sono dispari l’associazione fallirà come Pb₁ ‘≠ Pb₂’ ≠ ∞.
Pertanto, Eve ha un tasso di successo del 25%.
CONSIDERAZIONI
Il 25% può sembrare basso, ma nella sicurezza informatica è decisamente alto. È stato inoltre dimostrato, tramite la definizione di un attacco molto più sofisticato, che il tasso di successo può raggiungere il 50%.
CONCLUSIONI
Al rilascio del Patch Tuesday, l’NSA e media hanno sminuito eventuali impatti causati da questa vulnerabilità, poiché non è di tipo remote code execution.
È bene invece ricordare che tale bug consente a un qualsivoglia malintenzionato lo spoofing della firma di un software, rendendo quest’ultimo legittimo in fase di esecuzione, con implicazioni deleterie per i nostri dispositivi.
È bene quindi applicare quanto prima il Patch Tuesday, ora che si sanno nel dettaglio i rischi che ne conseguono in caso di esposizione.
Fonti
https://medium.com/hackernoon/bluetooth-hacking-cheating-in-elliptic-curve-billiards-c092fdf70aae
https://krebsonsecurity.com/2020/01/cryptic-rumblings-ahead-of-first-2020-patch-tuesday/
Note
[1] Esperto di sicurezza presso il CERT-CC.
[2] Di Brian Krebs.
[3] http://www.di-srv.unisa.it/~ads/corso-security/www/CORSO-0102/CAPICOM/CryptoAPI.htm
[4] https://www.youtube.com/watch?v=dCvB-mhkT0w
Articolo a cura di Daniele Rigitano

Laureato in Tecnologie Informatiche e con un Master in Sicurezza delle Reti.
Da sempre appassionato di Sicurezza Informatica e vicino alle tematiche come Threat Intelligenze, Computer Fosensics ed Information Security Management, entra come Cyber Security Specialist nel Computer Emergency Response Team del Ministero dell'Economia e delle Finanze.