Bias nell’Intelligenza Artificiale: Strategie e Norme ISO per la Valutazione e il Controllo
I sistemi AI trovano ormai dilagante applicazione in ogni ambito della nostra vita e cultura attraverso, ad esempio, i modelli di Machine Learning (ML), ma, come molte volte accade, non si hanno informazioni chiare su come il modello abbia “imparato” e prodotto un determinato output.
Ecco, quindi, come un sistema di gestione dedicato all’AI può costituire un importante strumento a supporto di una corretta governance e controllo di tali modelli.
A tal proposito, la norma ISO 42001:2023 introduce molti di questi concetti, come nel caso della clausola 9.1, che individua proprio gli indicatori dedicati, o dei controlli previsti dall’Allegato A, che riportano la necessità di avere la contezza dei risultati: i controlli della classe A.6.2, da esempio, richiedono la verifica e la validazione delle misure.
Altro punto focale, sempre oggetto di richiamo quando si ragiona in punto di sistemi intelligenti, è quello che va a toccare i concetti di analisi dei rischi e di valutazione d’impatto.
A supporto dello standard ISO/IEC 42001:2023 Sistema di Gestione dell’AI ci sono altre norme che guidano ad una corretta analisi e implementazione dei controlli, quali
- la norma ISO/IEC 42005 – Tecnologia dell’informazione — Intelligenza artificiale (AI) Valutazione d’impatto dei sistemi IA, e
- la ISO/IEC 23894, Information technology — Artificial intelligence — Risk Management.
Con riferimento, specificamente, ai modelli di ML e alla loro verifica, possono venire in aiuto alcune norme dedicate, comprese quelle sulla qualità dei dati, come ad esempio:
- ISO/IEC 4213 Information technology — Artificial intelligence — Assessment of machine learning classification performance,
- ISO/IEC 6254 Information technology — Artificial intelligence — Objectives and approaches for explainability of ML models and AI systems,
- ISO/IEC 23053 Framework for Artificial Intelligence (AI) Systems Using Machine Learning (ML), e
- ISO/IEC 5259 1-5 Data quality for analytics and machine learning (ML) ISO/IEC 5339.
Dal momento che, come si è accennato ed è ormai noto, una delle problematiche intrinseche più rilevanti dei sistemi algoritmici è – a tutt’oggi – costituita dalla loro opacità e scarsa comprensibilità, è evidente come sia sempre più necessario affidarsi a specifiche metodologie al fine di meglio comprendere la correttezza del modello in uso.
Ancora di più se si pensa ad un ulteriore aspetto di complessità dell’AI, ossia quello che coinvolge la distorsione algoritmica o bias, intesa come forma di distorsione cognitiva causata dal pregiudizio in grado di influenzare ideologie, opinioni e comportamenti. Il bias è, per semplificare, un errore nel processo di apprendimento che deriva da assunzioni errate.
Con il precipuo scopo di indagare tale specifico aspetto è nata la ISO 24027:2021, che descrive metodologie e meccanismi per scoprire e trattare i bias nei sistemi di intelligenza artificiale, che vengono descritti, nelle definizioni, come:
- “bias”, ossia una differenza sistematica nel trattamento[1] di determinati oggetti, persone o gruppi rispetto ad altri;
- “bias cognitivo umano”[2], che si verifica quando gli esseri umani elaborano e interpretano le informazioni;
- “bias di conferma”, quel tipo di bias cognitivo umano che favorisce le previsioni dei sistemi di intelligenza artificiale che confermano credenze o ipotesi preesistenti.
Nel documento si analizzano varie fonti di distorsioni indesiderate nei sistemi di AI, ricondotte a 3 categorie principali (distorsioni cognitive umane; distorsioni dei dati; distorsioni introdotte da decisioni ingegneristiche), così come il trattamento delle stesse durante i singoli stadi del ciclo di vita del sistema intelligente, a partire dalla raccolta dei dati, per passare alla progettazione, allo sviluppo, alle fasi di test e. arrivare al monitoraggio e alla validazione continui.
Sebbene si tenda ad attribuire al concetto di distorsione sempre un’accezione negativa, la norma in oggetto apre spiegando che, in realtà, gli effetti dei bias possono essere positivi, neutri o negativi, come si è cercato di sintetizzare nella tabella che segue:
| Effetto positivo | L’introduzione di errori/bias può servire a raggiungere un risultato equo. | Ad esempio, l’introduzione di una distorsione nella fase decisionale di un processo di selezione di personale con date caratteristiche al fine di compensare “tare” nei data set dovute alla sottorappresentazione consolidata nel tempo di tali professionalità. |
| Effetto neutro | La distorsione porta il sistema intelligente a classificare erroneamente un dato elemento, ma senza impatti particolari. | Ad esempio, una vettura a guida autonoma riconosce come ostacolo un cassonetto, ma lo classifica erroneamente come idrante. |
| Effetto negativo | Il bias porta con sé conseguenze indesiderate (etici o non ricadenti su profili etici) | Ad esempio, può limitare le opportunità delle persone interessate (distorsioni che favoriscono candidati di un sesso piuttosto che di un altro) o incidere negativamente nella classificazione di qualcosa (es. una galassia) |
Ciò premesso, resta tuttavia evidente come la perplessità prevalente relativa ai pregiudizi sia la facilità con cui gli stessi possono propagarsi in un sistema, a cui corrisponde – per contro – la difficoltà di riconoscerli e mitigarli. Tale aspetto va peggiorando tanto più il sistema è automatizzato (e tante più AI contribuiscono all’automazione), poiché in tal caso la supervisione umana diventa sempre meno efficace e, quindi, i bias negativi (anche involontari) trovano una facile via di sopravvivenza.
È bene evidenziare come mentre è decisamente probabile che in un sistema possano essere rintracciate più fonti di bias contemporaneamente, è, invece, assai improbabile che l’analisi di un sistema possa rilevarli tutti.
Alla luce di tutto quanto sopra descritto e in particolare con riferimento alle metodologie applicabili, si ritiene, quindi, di una certa utilità soffermarsi sulla cd. “matrice di confusione”, che costituisce uno strumento per analizzare gli errori compiuti da un modello di machine learning.
Nello specifico, come evidenzia la ISO 24027:2021, tale matrice riporta il numero di falsi positivi, falsi negativi, veri positivi e veri negativi e include ulteriori criteri di prestazione derivati da questi valori, come riportato nell’immagine seguente
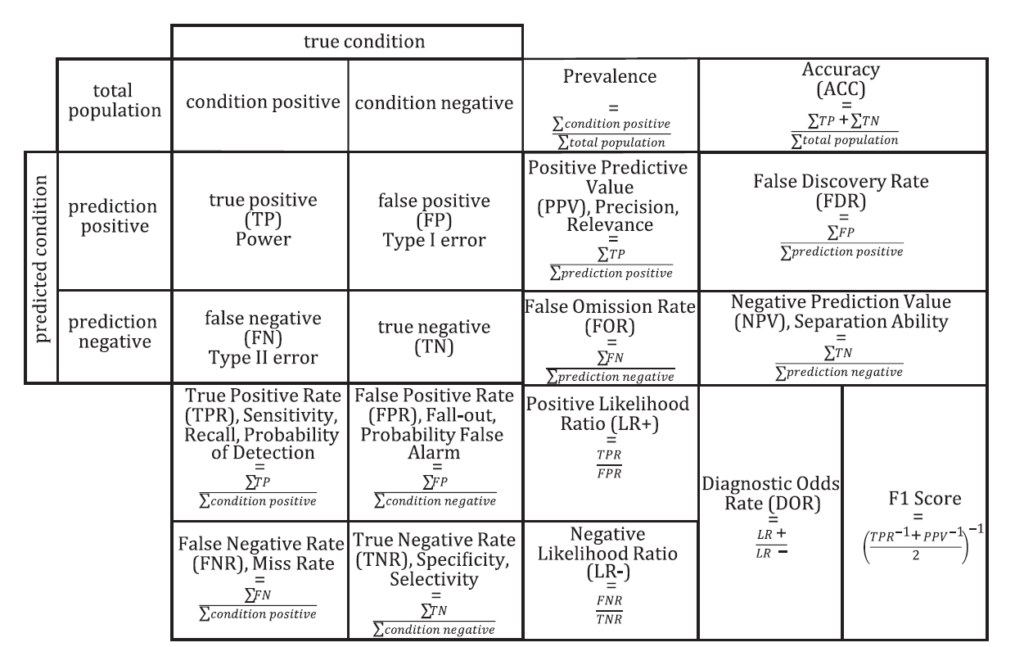
Poiché una matrice di confusione contiene e confronta più parametri, consente un’analisi dettagliata delle prestazioni di un classificatore ed è utile per aggirare o scoprire i punti deboli dei singoli parametri.
Consideriamo per semplicità un classificatore binario dove le classi si identificano con SI e NO.

Dove Tp = Veri Positivi, Fn = Falsi Negativi, Fp = Falsi Positivi e Tn = Veri Negativi.
Ad esempio, il modello analizza 100 risultati (identificazione di immagini di animali: cane e gatto) e le classifica come risultati veri o falsi. In 70 casi il modello classifica correttamente (cani) mentre in 30 sbaglia (gatti).

Come indicato nella figura 1, possono verificarsi quattro casi:
- True positive (Tp)
Se la classe prevista è SI nella prima riga e prima colonna ed è uguale alla classe effettiva il modello ha risposto correttamente SI.
- True negative (Tn)
Se la classe prevista è NO nella seconda riga e seconda colonna ed è uguale alla classe effettiva, il modello ha risposto correttamente NO.
- False positive (Fp)
Se la classe prevista è SI ma è diversa dalla classe effettiva, quindi nella seconda riga e prima colonna, il modello ha sbagliato a rispondere SI.
- False negative (Fn)
Se la classe prevista è NO ma è diversa dalla classe effettiva, cioè prima riga e seconda colonna, il modello ha sbagliato a rispondere NO.
Per soddisfare anche i controlli delle norme e le guide dalle norme ISO sopra citate è opportuno introdurre le metriche di una matrice di confusione.
- Accuratezza: l’accuratezza complessiva del modello, definita come il rapporto tra le previsioni corrette e il numero totale di previsioni. Indica la proporzione di esempi che sono stati previsti correttamente.
- Precisione: la precisione del modello, definita come il rapporto tra i veri positivi e il numero totale di esempi previsti come positivi. Indica la proporzione di esempi previsti come positivi e che sono effettivamente positivi.
- Richiamo: il richiamo del modello, definito come il rapporto tra i veri positivi e il numero totale di esempi effettivamente positivi. Indica la proporzione di esempi positivi che sono stati previsti correttamente come positivi.
- Punteggio F1: il punteggio F1 è una media ponderata della precisione e del richiamo ed è calcolato come. Fornisce un’unica metrica che bilancia sia la precisione che il richiamo.
- Specificità (Specificity):La specificità rappresenta la proporzione di veri negativi rispetto al totale delle istanze negative effettive. Misura quanto il modello è bravo a identificare le istanze negative.
- ROC Curve (Receiver Operating Characteristic Curve):La curva ROC è un grafico che mostra la relazione tra il tasso di veri positivi e il tasso di falsi positivi al variare della soglia di classificazione. A mano a mano che la soglia varia, i punti ROC vengono disegnati e collegati, e l’area sotto la curva ROC (AUC) può essere utilizzata come misura dell’efficacia del modello.
Accuratezza
L’accuratezza misura la percentuale delle previsioni esatte sul totale delle istanze. È l’inverso del tasso di errore. È compreso tra 0 (peggiore) e 1 (migliore). Essa indica quante volte il nostro modello ha correttamente classificato un item nel nostro dataset rispetto al totale.
Infatti, la formula per l’accuratezza è la divisione tra numero di risposte corrette e il totale delle risposte. Vale a dire che non ci permette di comprendere il contesto nel quale stiamo operando.
Deve essere sempre considerata nel contesto del modello. Ad esempio, è sconsigliato usare la accuratezza come metrica di valutazione quando operiamo con un dataset sbilanciato, dove le classi sono distribuite in maniera impari. Se la accuratezza non è altro che il rapporto tra risposte corrette sul totale, allora se una classe compone il 90% del nostro dataset e il nostro modello (erroneamente) classifica ogni esempio nel dataset con quella classe specifica, allora la sua accuratezza sarà del 90%.
Si potrebbe quindi pensare che il modello sia molto performante, quando in realtà è molto lontano dall’esserlo.
ACC = (Tp+Tn)/(Tp+Tn+Fp+Fn) = 1 – ERR (1)
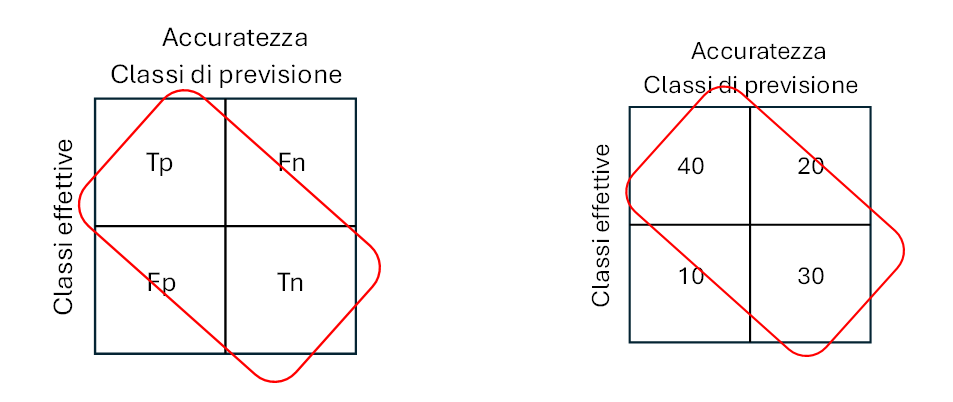
dove ERR è il tasso di errore, cioè, misura la percentuale di errore delle previsioni sul totale delle istanze. È compreso tra 0 (migliore) e 1 (peggiore).
ERR = (Fp+Fn)/(Tp+Tn+Fp+Fn) (2)
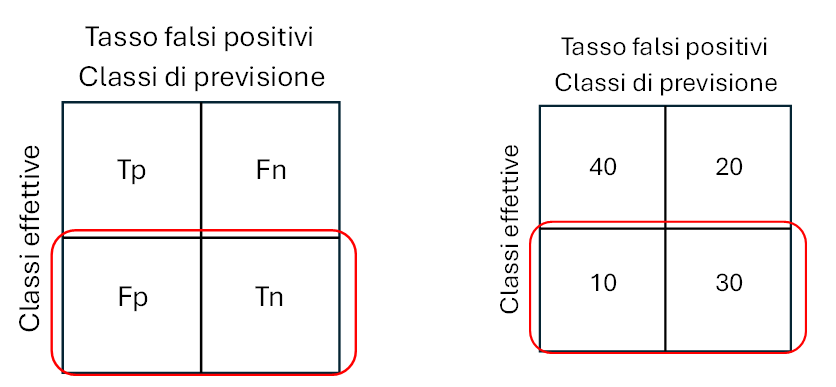
Precisione
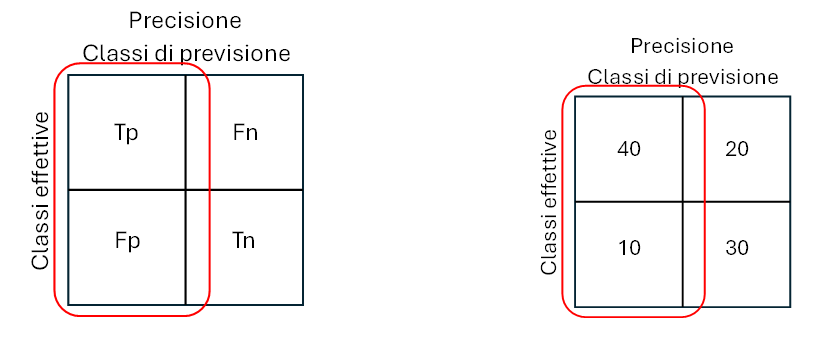
La precisione è la percentuale delle previsioni positive corrette (Tp) sul totale delle previsioni positive del modello (giuste Tp o sbagliate Fp).
La precisione non è altro che l’accuratezza calcolata solo per classi positive. Essa è anche chiamata specificità positiva poiché definisce quanto sensibile è uno strumento quando c’è il segnale da riconoscere. Di fatto, la metrica ci informa quanto spesso siamo corretti quando classifichiamo una classe come positiva.
Un modello con alta precisione ci allerterà poche volte, ma quelle volte che lo farà possiamo essere abbastanza sicuri che si tratti veramente di un dato inteso come intruso.
Pr = Tp/(Tp+Fp) (3)
Richiamo o sensitività
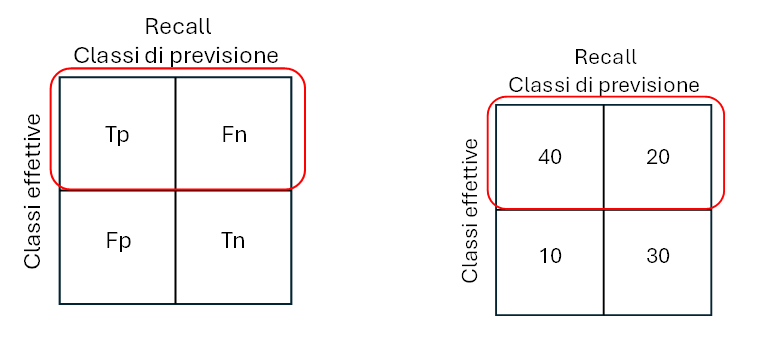
Il richiamo o sensitività è la percentuale delle previsioni positive corrette (Tp) sul totale delle istanze positive. È compreso tra 0 (peggiore) e 1 (migliore). Se siamo interessati a riconoscere quanti più classi positive possibili, allora il nostro modello dovrà avere un richiamo alto.
In pratica significa che qui dobbiamo tener conto dei falsi negativi invece dei falsi positivi. Il richiamo viene anche chiamato sensibilità perché all’aumentare del richiamo, il nostro modello diventa sempre meno preciso e classifica anche classi negative come positive.
Un modello ad alta precisione è conservativo, ma introduce anche molto rumore di fondo.
Risulta quindi impossibile avere un modello con alta precisione e alto richiamo. Infatti, queste due metriche sono complementari: se aumentiamo una, l’altra deve diminuire. Si tratta del precision/recall trade-off.
Rec = Tp/(Tp+Fn) (4)
Specificità
La specificità è la percentuale delle previsioni negative corrette (Tn) sul totale delle istanze negative. È compresa tra 0 (peggiore) e 1 (migliore).
Sp = Tn/(Tn+Fp) (5)

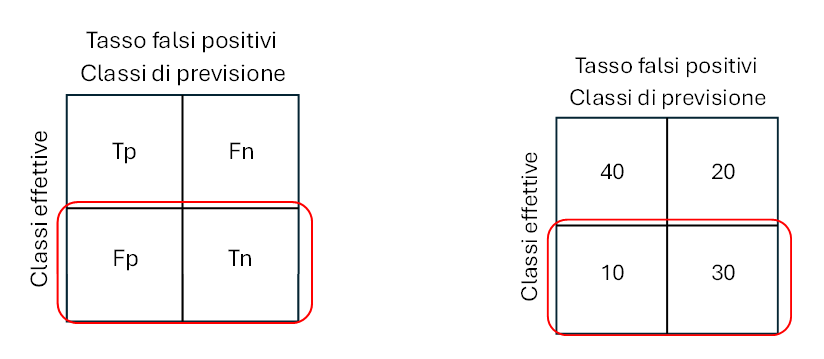
Tasso dei falsi positivi
Il tasso dei falsi positivi (False Positive Rate) è la percentuale delle previsioni positive errate (Fp) sul totale delle istanze negative. Compreso tra 0 (migliore) e 1 (peggiore).
Fpr = Fp/(Tn+Fp) (6)
Punteggio F
Il punteggio F (F-Score) è la media armonica delle metriche Precision e Recall. Varia da 0 (peggiore) a 1 (migliore).
A questo punto è chiaro che usare precisione o richiamo come metrica di valutazione è difficile perché possiamo solo usarne una a scapito dell’altra. Il punteggio F1 risolve proprio questo problema. Il punteggio F1 combina precisione e richiamo in una sola metrica. Questa è la media armonica di precisione e richiamo, ed è probabilmente la metrica più usata per valutare modelli di classificazione binaria. Se il punteggio F1 aumenta, vuol dire che il modello ha aumentato le performance per precisione, richiamo o per entrambi
F1 = (2* Rec*Pre)/Rec+Pre (7)
Nell’esempio: Punteggio F = (2*Recall*Precisione)/(Recall+Precisione) = 0.73 (8)
ROC-AUC
La metrica ROC-AUC si basa su una rappresentazione grafica della curva ROC (receiving operating characteristic curve).
“le curve ROC […] sono degli schemi grafici per un classificatore binario. Lungo i due assi si possono rappresentare la sensibilità e (1-specificità), rispettivamente rappresentati da True Positive Rate (TPR, frazione di veri positivi) e False Positive Rate (FPR, frazione di falsi positivi). In altre parole, si studiano i rapporti fra allarmi veri (hit rate) e falsi allarmi.” Tratto da Wikipedia
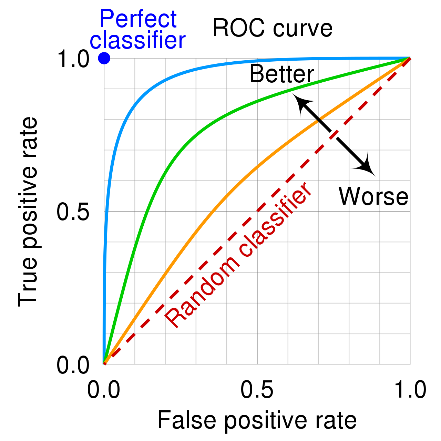
AUC significa Area Under the Curve (area al di sotto della curva). Se poniamo l’attenzione sulla linea blu, vediamo che al di sotto di essa c’è di fatto una area più grande rispetto alle linee verde arancione. La linea tratteggiata indica una metrica di ROC-AUC del 50%.
Di conseguenza un buon modello avrà una ROC-AUC grande, mentre un modello scarso si posizionerà vicino alla linea tratteggiata, che non è altro che un modello che risponde in maniera casuale.
La metrica ROC-AUC è anche molto utile per confrontare diversi modelli uno contro l’altro.
Coefficiente di correlazione di Matthews (MCC)
Questo serve per valutare correttamente anche modelli addestrati su dataset non bilanciati.
La formula si comporta come un coefficiente di correlazione. Essa è compresa tra +1 e -1. Un valore che tende a +1 misura la qualità delle predizioni del nostro classificatore anche in contesti con classi sbilanciate nel dataset, poiché indica una correlazione tra valori reali osservati e previsioni fatte dal nostro modello.
MCC = [(Tp*Tn)-(Fp*Fn)]/ Ö[(Tp+Fp)*(Tp+Fn)*(Tn+Fp)*(Tn+Fn)] (9)
Ma possiamo fare un ulteriore passo avanti.
Possiamo introdurre, altri calcoli di verifica, coinvolgendo calcoli algebrici e la meccanica quantistica. In particolare, introduciamo il quadrato di un binomio
(a+b)2 = a2+ b2+2*a*b (10)
dove, i quadrati sono considerati la probabilità di accadimento e il doppio prodotto è l’interferenza.
Quindi possiamo estendere le formule sopra citate (recall, sensibilità, etc.) e considerando il rapporto tra il doppio prodotto e la somma dei quadrati
2ab/a2+b2 (11)
ottenendo:
Precisione:
InPr = (2*Tp*Fp)/(Tp2+Fp2), che nell’esempio assume il valore 0.47 (12)
Recall:
InRec = (2*Tp*Fn)/(Tp2+Fn2), che nell’esempio assume il valore 0.8 (13)
Specificità:
InSp = (2*Tn*Fp)/(Tn2+Fp2), che nell’esempio assume il valore 0.6 (14)
Queste formule forniscono il rapporto tra l’interferenza e la somma di probabilità.
Per concludere, dunque, per raggiungere una visione ed un controllo completi dei sistemi di intelligenza artificiale, pare imprescindibile puntare alla conoscenza tanto della parte umanistica, etica, psicologica e giuridica, quanto della componente più prettamente tecnica, che a sua volta non potrà prescindere dal supporto fornito dagli standard di settore, in parte qui analizzati.
Note
[1] Il trattamento è qualsiasi tipo di azione, inclusa la percezione, l’osservazione, la rappresentazione, la previsione o la decisione.
[2] i pregiudizi cognitivi umani influenzano il giudizio e il processo decisionale.
Articolo a cura di Stefano Gorla e Avv. Anna Capoluongo